Crystal System & Bravais Lattices

Crystal system and Bravais lattices-

 Crystal system and Bravais lattices-

Based upon the dimensions of the unit cells (i.e. length a, b, and c and the angles (α , β and γ ) there are seven types of unit cells. These are also called crystal systems are crystal habits because any crystalline solid must belong to any one of the unit cells.

“At first sight there seems to be infinite number of shapes of crystals. However careful examination of several thousand crystals of various substances has revealed that only seven possible symmetries are possible. The seven different combinations of symmetry elements are called crystal systems.” 

These crystal systems differ in the length of the unit cell edges (a, b and c) and angles ( α,
β and γ ) between the unit cell The arrangement of particles in the study of crystal was first given by German Scientist M. Frankenheim in 1844.

Classification on the basis of geometrical consideration-

 In 1848 A. Bravais studied geometrical arrangement of crystals on the basis of three fundamental rules of crystallography According to Bravais there are 14 space lattices are possible in several thousand crystals. In other words lattice points are arranged in space by 14 specific combinations.

A.Bravais is also called as father of chemical crystallography.

“ The fourteen lattices corresponding to seven crystal systems are known as Bravais lattices.” 
                                                 
  Seven types of unit cells  or crystal system
     

According to a, b and c and α ,β and  γ 
 there may be 230 possible shapes which are grouped in to 32 classes, these 32 classes are again grouped into 14 Bravais lattices, which collectively form 7 crystal system


Co-ordination Number-

The number of oppositely charged ions surrounding a particular ion in the ionic crystal is called its co-ordination number or Gold-Smidt number. The concept was given by Goldsmidt and Alfred Werner. 

It is the characteristics of a space lattice  and its value can be calculated by observing the crystal lattice.

The value of co-ordination number of simple cubic lattice (SC) is 6

The value of coordination no of BCC is 8

The value of co-ordination number of face centred cubic (FCC) is 12.


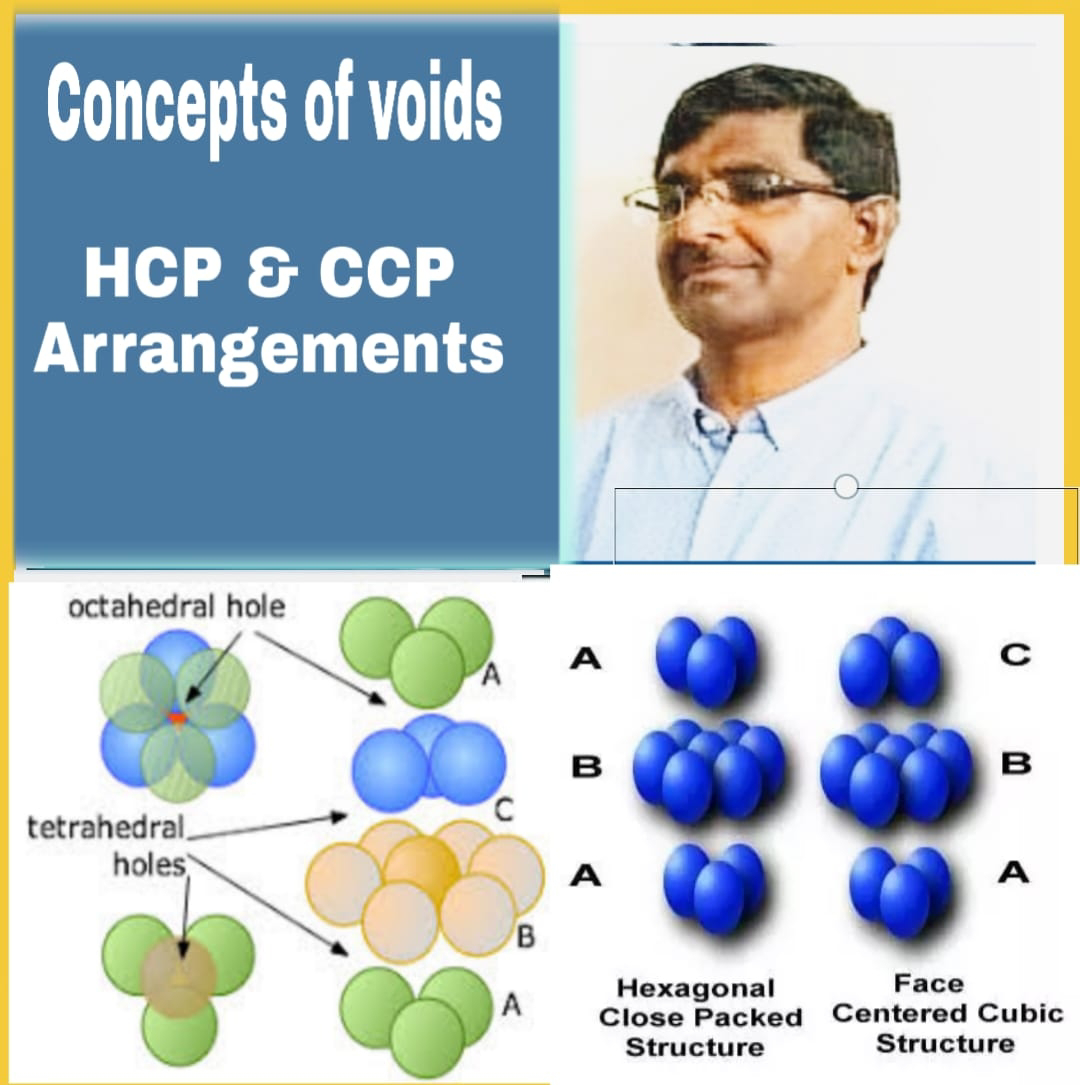
The value of co-ordination number of hexagonal closed packing (HCP) and cubic closed packing (CCP) is 12.


Popular posts from this blog

Tertahadral & Octahedral Voids, HCP & CCP

Image
Concepts of Voids, HCP & CCP Arrangements Density of unit cell- Tetrahedral and Octahedral void-  Tetrahedral Void-                                                                              A simple triangular void in a crystal which is surrounded by four spheres is called tetrahedral void. A tetrahedral void is developed when triangular voids have contact with one sphere either in the upper layer or in the lower layer. Tetrahedral void means the tetrahedral arrangement of spheres.                                            .     Characteristics of tetrahedral void- (i) Ratio of radii of void and constituent particle is constant.   r/R = 0.225 (ii) Co-ordination number  of particle present in the void is 4 (iii) Each constituent particle makes two tetrahedron with three spheres above and three spheres below (iv) No. of tetrahedral voids    = 2 ×No. of atoms    = 2× octahedral voids Relationship B/W  radius of void (r) and radius o
Read more

Basic Concepts of Chemical Crystallography

Image
CHEMICAL CRYSTALLOGRAPHY- A branch of physical science that deals with the study of crystals i.e. their source, classification, properties and structure etc. is called chemical crystallography. A crystalline solid consist of a large number of small units called crystal. A crystal is a solid figure with a definite geometrical shape, flat faces and sharp edges. Crystal lattice and unit cell- “Regular arrangement of constituent particles i.e. atoms, ions or molecules of a crystal in a three dimensional space is called crystal lattice or space lattice.” “The smallest three dimensional portion of a complete space lattice which when repeated over and again in different directions to generate the complete space lattice is called the unit cell”       The situation may be compared with that of a thick wall made up of bricks, where brick is similar to the unit cell and the wall to the complete space lattice. The unit cell may be considered as the fundamenta
Read more

Relation between nearest neighbour distance and radius of atom, Concept of Radius ratio

Image
Relationship between the nearest neighbour distance (d), edge of the unit cell (a) and the radius of the atom (r) (1)Simple cubic unit cell- Distance between nearest neighbour (d) = AB = a Hence for simple cubic (SC)  d = a   and r = a/2 (2)Face centred cubic unit cell-    Distance between nearest neighbour (d) =  AC (Because spheres at the face diagonal are touching each other)    But from  ∆ ABC      AC2 = AB2 + BC2                       Hence        d = a2 + a2                                  d =  2a2                             d =  √2a                             d =a/ √2   Since atomic radius (r = d/2)                                      r=  AC/2 = a/2√2                                                                    Hence for face centred cubic (FCC)  d =a√2         and   r =  a/2√2 (3) Body centred cubic unit cell- The distance between nearest neighbour (d) = 1/2 CD  Since all the spheres at the corners touch the central sphere, so CD
Read more